Paralelismo

PARALELISMO

 

Rectas Paralelas entre sí

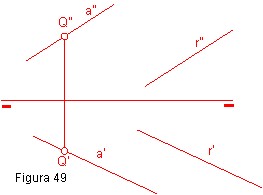
Si dos rectas a y r son paralelas en el espacio, sus proyecciones homónimas (vertical y horizontal) también son paralelas. Recíprocamente cuando dos rectas tienen sus proyecciones tanto horizontales como verticales paralelas, éstas son paralelas en el espacio.

Por ejemplo, por un punto Q pasar una recta a paralela a una recta r. 

Recta Paralela a un Plano

Una recta es paralela a un plano cuando es paralela al menos a una recta contenida en dicho plano. Si la recta no cumple otra condición hay infinitas soluciones.

Por ejemplo:

Se dibuja una recta s cualquiera contenida en el plano a. Para que una recta esté contenida en un plano las trazas vertical y horizontal de la recta cualquiera s deben estar en las trazas del plano a respectivamente.

Luego por un punto dado se traza la recta r paralela a la recta s del plano.

 

Planos Paralelos

Al ser cortados dos planos paralelos por un tercer plano, las rectas de intersección son necesariamente paralelas entre sí.

Condición necesaria y suficiente para que dos planos sean paralelos, es que sus trazas diédricas sean paralelas respectivamente, es decir, un plano es paralelo a otro cuando sus trazas homónimas lo son.

Por ejemplo:

Dado el plano P y el punto A, hallar un plano Q paralelo a P que pase por A:

En este caso, como sabemos que las trazas del plano son paralelas, nos bastará con hallar una recta r en el plano P, en este caso por su facilidad se trazará una recta frontal u horizontal. Se hace una paralela que pase por A, y mediante la traza de la nueva recta paralela, hacemos las trazas del plano paralelas a las del plano P.

Investigar: 

¿Cómo se halla una recta paralela a una recta de perfil?

Proyección de una Recta

La recta es el rastro que deja un punto sobre el espacio cuando este se mueve en una dirección y pendiente constante.

En el espacio la línea recta está definida, bien sea por dos puntos o un punto y una dirección. Se acostumbra a denominar la recta con la letra minúscula

Representación de una recta dada por dos puntos en el espacio (A y B) Ejemplo: 

Según la posición de la recta con respecto a los planos de proyección (horizontal, vertical o frontal y de perfil) esta puede recibir diferentes denominaciones.

Tipos de rectas: De Pie AB, De Punta CD, Frontal EF, Paralela a la L.T. MN, Horizontal GH, Oblicua IJ, De Perfil KL.

Recta de Pie (AB): Es perpendicular al plano horizontal.

Recta de Punta (CD): Es perpendicular al plano vertical o También llamado frontal.

Recta frontal (EF): Es paralelo al plano vertical o también llamado frontal.

Recta paralela a la L.T. Es paralelo a la línea de tierra.

Recta Horizontal (GH): Es paralelo al plano horizontal.

Recta oblicua (IJ): No es paralela al PH, PV y PL.

Recta de Perfil (LK): Es paralela al plano lateral o plano de perfil.  

Representación en doble proyección ortogonal: 

                                                       Recta Frontal:

  

Recta de Punta:

Recta Vertical:

Recta Horizontal:

Recta Paralela a la línea de tierra (L.T.) :

 Recta de Perfil:

  Trazas de la recta:  La traza (o intersección) es el punto de penetración de una recta en un plano de proyección también se denomina puntos trazas o puntos notables de la recta. Para que un punto (como el punto traza) pertenezca a la recta debe tener su proyección sobre la proyección de la recta.

 La traza vertical: Se determina con la intersección de la proyección horizontal con la línea de tierra encontrando el punto V (V h =0) donde corta con la proyección vertical.

Y la traza horizontal: Se determina con la intersección de la proyección vertical con la línea de tierra encontrando el punto H (H v =0) donde corta con la proyección horizontal.

Ejemplo: 

 En doble proyección ortogonal:

Investigar: ¿cómo se halla la visibilidad de un elemento geométrico? y ¿cómo se representa en doble proyección ortogonal?. Por otro lado, ¿cómo se halla la dirección de una recta en doble proyección ortogonal?