Perpendicularidad

PERPENDICULARIDAD

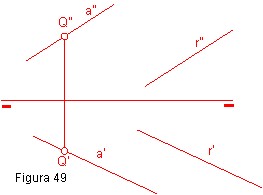
Recta Perpendicular a un Plano

Si se requiere trazar por un punto dado una recta que sea perpendicular a un plano, se deberá por cada proyección del punto (horizontal y vertical) trazar la recta perpendicular a la traza homónima del plano. Así siendo el punto O y el plano dado por sus trazas, que son rectas características del plano, es decir, horizontal y frontal.

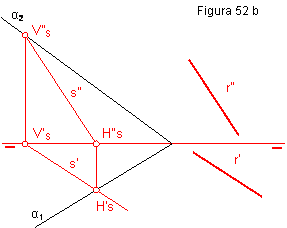
La recta así obtenida es la solución única. Si el punto pertenece al plano, deberá estar contenido en una horizontal o frontal de dicho plano, de ser exterior a dicho plano se resuelve de forma idéntica. Trazando por sus proyecciones las perpendiculares a las trazas, aunque el punto dado ya no sería el de intersección de la recta y el plano.

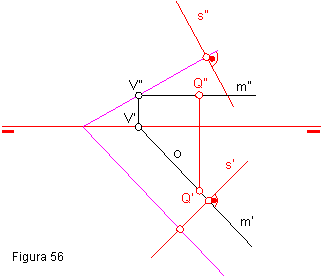
Plano Perpendicular a una Recta

Se requiere trazar un plano que sea perpendicular a una recta, entonces dado un punto Q y una recta s, se deberá por cada Q trazar una recta horizontal del plano, que se llamará m y será perpendicular a la recta s.

Luego se halla la traza vertical de la recta m y por esa proyección vertical de la traza, se trazará una perpendicular a la recta s, entonces se tendrá un plano perpendicular a una recta dada.  

Investigar:

¿Cómo se hallan dos rectas perpendiculares entre sí?

Si se quieren hallar dos planos perpendiculares, ¿cuántas soluciones hay? Y por qué?

Paralelismo

PARALELISMO

 

Rectas Paralelas entre sí

Si dos rectas a y r son paralelas en el espacio, sus proyecciones homónimas (vertical y horizontal) también son paralelas. Recíprocamente cuando dos rectas tienen sus proyecciones tanto horizontales como verticales paralelas, éstas son paralelas en el espacio.

Por ejemplo, por un punto Q pasar una recta a paralela a una recta r. 

Recta Paralela a un Plano

Una recta es paralela a un plano cuando es paralela al menos a una recta contenida en dicho plano. Si la recta no cumple otra condición hay infinitas soluciones.

Por ejemplo:

Se dibuja una recta s cualquiera contenida en el plano a. Para que una recta esté contenida en un plano las trazas vertical y horizontal de la recta cualquiera s deben estar en las trazas del plano a respectivamente.

Luego por un punto dado se traza la recta r paralela a la recta s del plano.

 

Planos Paralelos

Al ser cortados dos planos paralelos por un tercer plano, las rectas de intersección son necesariamente paralelas entre sí.

Condición necesaria y suficiente para que dos planos sean paralelos, es que sus trazas diédricas sean paralelas respectivamente, es decir, un plano es paralelo a otro cuando sus trazas homónimas lo son.

Por ejemplo:

Dado el plano P y el punto A, hallar un plano Q paralelo a P que pase por A:

En este caso, como sabemos que las trazas del plano son paralelas, nos bastará con hallar una recta r en el plano P, en este caso por su facilidad se trazará una recta frontal u horizontal. Se hace una paralela que pase por A, y mediante la traza de la nueva recta paralela, hacemos las trazas del plano paralelas a las del plano P.

Investigar: 

¿Cómo se halla una recta paralela a una recta de perfil?