CUERPOS REDONDOS
Un sólido de cuerpo redondo es aquel cuya superficie
generada puede ser reglada, es decir, de simple curvatura o de doble curvatura.
Los primeros se presentan cuando la generatriz
movida es una línea recta y se subdividen en desarrollables, como el cono y el cilindro o
alabeada, como el cilindroide, el conoide, el helicoide, el hiperboloide, entre
otros.
Los segundos se presentan cuando no se puede
trazar líneas rectas sino que las superficies son producidas por movimiento de
generatrices curvas y pueden ser de revolución como la esfera, el elipsoide, el
paraboloide, el hiperboloide, el anuloide o no son de revolución como el
espiral o serpentín, el toro espiral helicoidal (caracola), el helicoide, el helizoide, entre otros.
1 .Los conceptos de: generatriz, directriz,
director, eje de revolución, y eje de simetría.
2 .Los conceptos de: superficie reglada,
superficie desarrollable, superficie alabeada, superficie simplemente reglada,
superficie doblemente reglada, sólido de revolución, sólido de no revolución o
de evolución.
3. Los conceptos de: cilindroide, conoide,
anuloide, elipsoide, y helicoide.
4. Para cada una de las superficies nombradas
conseguir un ejemplo de la vida diaria.


21 comentarios:
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.
La generatriz1 es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal.
Una directriz se dice de aquello que marca las condiciones en que se genera algo.1
En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz).2
Si la directriz es una línea recta, y la generatriz es otra línea recta que gira en torno a ella, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es curva genera esferas, elipsoides, etc. Si la generatriz se desplaza sobre una o más directrices, genera una superficie reglada.
generatriz1 es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.
La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal
Una directriz se dice de aquello que marca las condiciones en que se genera algo.1
En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz).2
Si la directriz es una línea recta, y la generatriz es otra línea recta que gira en torno a ella, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es curva genera esferas, elipsoides, etc. Si la generatriz se desplaza sobre una o más directrices, genera una superficie reglada.
La directriz puede ser una línea curva, por ejemplo, una circunferencia generatriz que rueda sobre otra circunferencia, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal
1 Elección de ejes
Una parte importante de la elección de un sistema de coordenadas lo forma la dirección de los ejes. Es importante señalar que la dirección de los ejes es la que nosotros queramos que sea. Nadie se encuentra un eje por la calle. No hay nada en la naturaleza que diga que el eje debe ser vertical.
Si, por ejemplo, tenemos dos cargas puntuales situadas a una distancia , y nada más, la elección obvia es tomar el eje como el que pasa por las dos cargas, independientemente de si en la figura aparece inclinado. ¿Por qué el y no el o el ? porque el eje desempeña un importante papel en cilíndricas y esféricas, cosa que no ocurre con los otros dos.
En cuanto al origen de coordenadas, que también es arbitrario, para este sistema de dos cargas, hay dos posibles elecciones sencillas: en una de las cargas, o en el punto medio entre ambas.
Por último, respecto al sistema de coordenadas más conveniente para este sistema, no es el de cartesianas, sino el de cilíndricas, ya que el sistema presenta lo que se denomina simetría de revolución.
2 Simetrías
Uno de los conceptos más fructíferos en física, pero también de los más delicados, es el de simetría. Este concepto es también esencial a la hora de elegir un sistema de coordenadas.
Todos estamos familiarizados con la simetría como algo asociado a los espejos. Este es un caso particular de simetría (la bilateral). Decimos usualmente que un sistema es simétrico si al reflejarlo en un espejo, el sistema sigue siendo el mismo.
El concepto de simetría que usaremos es una generalización de este: decimos que un sistema posee una determinada simetría cuando al efectuar una cierta transformación (geométrica, o cambiando las coordenadas), el sistema no cambia.
Los ejemplos más frecuentes que encontraremos son:
2.1 Simetría traslacional
Es la que aparece cuando el sistema no cambia al desplazarnos en línea recta.
Por ejemplo, un hilo cargado de longitud infinita se ve siempre igual si nos movemos paralelamente a él.
Un sistema de dos cargas puntuales no posee simetría traslacional, ya que no es lo mismo estar cerca de una carga que cerca de la otra, o lejos de ambas.
Matemáticamente se expresa tomando como eje el del desplazamiento y estableciendo que el sistema no depende de la coordenada .
2.2 Simetría acimutal (o de revolución)
Aparece cuando el sistema no cambia al efectuar una rotación en torno a un eje fijo.
En el caso de dos cargas puntuales tenemos simetría acimutal, ya que al girar en torno a la recta que pasa por las dos cargas vemos siempre el mismo sistema.
Un sistema de tres cargas no alineadas no posee simetría acimutal.
Matemáticamente se expresa tomando el eje como el de revolución, y eligiendo coordenadas cilíndricas (o esféricas). La simetría acimutal equivale a decir que el sistema no depende de la coordenada .
2.3 Simetría esférica
Se produce cuando el sistema es invariante en torno a cualquier rotación en torno a un punto fijo.
Un ejemplo lo constituye una esfera cargada uniformemente.
Matemáticamente se expresa empleando coordenadas esféricas y afirmando que el sistema no depende ni de ni de .
Un mismo sistema puede presentar varias simetrías. Por ejemplo:
• Un hilo infinito posee tanto simetría traslacional como acimutal.
• Dos hilos infinitos paralelos solo traslacional, pero no acimutal.
• Un segmento finito posee simetría acimutal pero no traslacional.
• Dos segmentos finitos paralelos, ninguna de las dos.
El concepto de simetría es delicado porque es fácil "encontrar" simetrías inexistentes y hacer simplificaciones incorrectas. También hay que ser cuidadoso, como veremos a lo largo del curso, porque la expresión matemática de la simetría presenta matices importantes.
Pero, con todas las precauciones necesarias, las simetrías son importantes porque simplifican enormemente la solución de los problemas.
Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
Definición y representación diédrica.
Las superficies regladas están generadas por el movimiento de una
recta. En las superficies no desarrollables las generatrices se cruzan, no se
cortan.
Las superficies regladas desarrollables se caracterizan porque las
generatrices pasan por un punto llamado vértice y se apoyan sobre una línea
denominada directriz. Si la directriz es poligonal es pirámide o prisma y si es
curva, cono o cilindro. Si el vértice es propio, es cono o pirámide y si es
impropio, es decir, está en el infinito, es cilindro o prisma (figura 1).
Figura 1: Superficies regladas desarrollables.
La representación diédrica de superficies regladas, se muestra en la
figura 2, apoyadas en el horizontal. Las superficies están limitadas por su
vértice propio y una base o por dos bases.
Figura 2: Representación diédrica de superficies regladas.
Para la visualización de las figuras se tienen en cuenta los siguientes
detalles:
V'
V''
A'' B'' D'' C''
A'
C'
D' A' D'
C'
A'' B'' D'' C''
E' H'
F' G'
E'' F'' G'' H''
V'
V''
O'
O''
O'
O''
Q'
Q''
g 3 '' g 4''
g1'' g 2''
g3' g 4 '
g 1'
g 2'
g 3''
g 1'' g2''
g 4 ''
g 3'
g 1'
g 4'
g 2'
B' B'
¥
Vértice
Generatrices
Directriz
Directriz
Generatrices
Vértice
Cono PirámideSuperficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
Definición y representación diédrica.
Las superficies regladas están generadas por el movimiento de una
recta. En las superficies no desarrollables las generatrices se cruzan, no se
cortan.
Las superficies regladas desarrollables se caracterizan porque las
generatrices pasan por un punto llamado vértice y se apoyan sobre una línea
denominada directriz. Si la directriz es poligonal es pirámide o prisma y si es
curva, cono o cilindro. Si el vértice es propio, es cono o pirámide y si es
impropio, es decir, está en el infinito, es cilindro o prisma (figura 1).
Figura 1: Superficies regladas desarrollables.
La representación diédrica de superficies regladas, se muestra en la
figura 2, apoyadas en el horizontal. Las superficies están limitadas por su
vértice propio y una base o por dos bases.
Figura 2: Representación diédrica de superficies regladas.
Para la visualización de las figuras se tienen en cuenta los siguientes
detalles:
V'
V''
A'' B'' D'' C''
A'
C'
D' A' D'
C'
A'' B'' D'' C''
E' H'
F' G'
E'' F'' G'' H''
V'
V''
O'
O''
O'
O''
Q'
Q''
g 3 '' g 4''
g1'' g 2''
g3' g 4 '
g 1'
g 2'
g 3''
g 1'' g2''
g 4 ''
g 3'
g 1'
g 4'
g 2'
B' B'
¥
Vértice
Generatrices
Directriz
Directriz
Generatrices
Vértice
Cono Pirámide
La generatriz : es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc
Directriz: es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen.
Eje de revolución : línea recta alrededor de la cual gira un cuerpo geométrico. El movimiento se llama "rotación" si el eje pasa a través del cuerpo, y "revolución" si el eje está situado fuera del cuerpo. Por la rotación de una superficie geométrica (revolución de su curva límite) alrededor de un eje se genera un "sólido (o cuerpo) de revolución.
Un eje de simetría: es una línea de referencia imaginaria que sirve para definir una simetría.
superficie reglada: es la generada por una recta, denominada generatriz, al desplazarse sobre una curva o varias, denominadas directrices.
Superficie desarrollable
Es una curva que se puede desarrollar sobre un plano sin cambiar su área. Un ejemplo incluye la superficie lateral de un cono. Por el otro lado, una superficie esférica no lo es.
Superficie alabeada: son las superficies generadas por una línea curva que se mueve en el espacio según una ley determinada y que actúa como generatriz de la misma; se subdividen en cuadricas de revolución, elípticas y otras.
Solido de revolución : Es obtenido al rotar una región del plano alrededor de una rectaubicada en el mismo, las cuales pueden o no cruzarse.
Cilindroide: es la superficie alabeada en la que la generatriz se desplaza manteniéndose paralela a un plano director y apoyada sobre dos directrices curvas
Conoide :es la superficie generada por una recta que se apoya en dos directrices (una cónica y una recta no coplanaria) manteniéndose paralela a un plano.
Un elipsoide: es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, son originadas por planos que contienen dos ejes cartesianos.
Generatriz: linea que se mueve de acuerdo con ciertas condiciones y cuyo lugar geométrico forma cierta superficie.
Directriz: linea recta o curva sobre la cual se apoya continuamente la generatriz.
Director: plano, al cual son paralelas las generatices.
Eje de revolucion: linea alrrededor de la cual rota la generatriz.
Eje de simetria: linea con respecto a la cual el cuerpo es simetrico.
superficie regladas: cuando la generatriz movida es una linea recta y que se subdivide en:
1) desarrollables
2)alabeadas
los desarrollables son: el cono y el cilindro (analogos a la piramide y prisma) y pueden ser : rctos ( el eje es perdpendicular a la base y pasa por su centro) y oblicuos.
superficie alabeada: es, por definicion, una superficie reglada, donde dos generatrices rectas, consecutivas no son paralelas, ni se cortan.
simplemente regladas: por cada punto pasa una generatriz recta.
Cilindroide: Generatriz recta que se apoya sobre dos directrices curvas y es paralela a un plano director.
conoide ( recto u oblicuo): Generatriz recta paralela al plano director, que se apoya sobre una directriz recta y otra curva.
Helicoide: (recto u oblicuo): Generatriz recta que se apoya sobre una helice conica o cilindrica y forma un angulo constante con ella o con un plano.
Doblementes regladas: superficies , donde por cada punto pasan dos generatrices rectas.
solidos de revolucion: generatriz curva que rota alrrededor de un eje. Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.
esfera, elipsoide, paraboloide, hiperboloide, toro o anilo.
La generatriz: es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.
Una directriz: se dice de aquello que marca las condiciones en que se genera algo.
En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz).2
Si la directriz es una línea recta, y la generatriz es otra línea recta que gira en torno a ella, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es curva genera esferas, elipsoides, etc. Si la generatriz se desplaza sobre una o más directrices, genera una superficie reglada.
Eje de revolucion: línea recta alrededor de la cual gira un cuerpo geométrico. El movimiento se llama "rotación" si el eje pasa a través del cuerpo, y "revolución" si el eje está situado fuera del cuerpo. Por la rotación de una superficie geométrica (revolución de su curva límite) alrededor de un eje se genera un "sólido (o cuerpo) de revolución"
El eje de simetría:es la mediatriz del segmento cuyos extremos son puntos simétricos. Matemáticamente, un eje de simetría de un conjunto geométrico es siempre una línea de puntos fijos invariante bajo un conjunto de operaciones del grupo de simetría del conjunto.
Para poder determinar intuitivamente el eje de simetría se puede tomar una hoja y dibujar una figura geométrica, sea o no regular (cualquier figura geométrica siempre que sea simetrizable), luego se empieza a doblar de manera que coincidan los trazos de ambas caras. El pliegue indicará entonces el eje.
Una superficie reglada, en geometría, es la generada por una recta, denominada generatriz, al desplazarse sobre una curva o varias, denominadas directrices. En función de las características y condiciones particulares de estos elementos, recibe diversos nombres.
Plot paramétrico de una banda de Möbius.
[editar]Clasificación de las superficies regladas
Superficies regladas son:
el plano
las superficies de curvatura simple:
superficie cilíndrica
superficie cilíndrica de revolución
superficie cilíndrica de no revolución
superficie cónica
superficie cónica de revolución
superficie cónica de no revolución
las superficies alabeadas
cilindroide
conoide
superficie doblemente reglada
paraboloide hiperbólico
hiperboloide de revolución.
uperficie desarrollable es la que se puede extender sobre un plano sin rotura ni deformación.
Las superficies desarrollables son uno de los dos tipos en los que se dividen las superficies regladas.
Superficie alabeada son las superficies generadas por una línea curva que se mueve en el espacio según una ley determinada y que actúa como generatriz de la misma; se subdividen en cuadricas de revolución, elípticas y otras.
La superficie alabeada es la superficie que no se puede superponer sobre un plano.
Las superficies alabeadas son uno de los dos tipos en los que se dividen las superficies regladas.
También se la denomina superficie no desarrollable o superficie curva.
Entre este tipo de superficies, se puede citar el cilindroide, el conoide y la superficie doblemente reglada.
Una superficie es de hecho un conjunto de puntos de un espacio euclídeo que forma un espacio topológico bidimensional que localmente, es decir, visto de cerca se parece al espacio euclídeo bidimensional. Así alrededor de cada punto de una superficie esta se aproxima bien por el plano tangente a la superficie en dicho punto.
Una definición tradicional de superficie que alude a términos intuitivos pero con la que resulta fácil trabajar desde un punto de vista matemático fue la dada por Euclides:
Una superficie es aquello que sólo tiene longitud y anchura.
Superficies desarrollables
Una banda de Möbius.
Un caso especial de la superficies regladas son las superficies desarrollables que, mediante deformaciones que no alteren las distancias entre sus puntos, pueden ser transformadas en un fragmento plano. Técnicamente existe una isometría entre estas superficies y un fragmento de plano. Decimos que es localmente desarrollable si existen isometrías locales; para que esto ocurra es necesario y suficiente que la curvatura gaussiana sea nula.
El cono, el cilindro y el propio plano son desarrollables, mientras que el hiperboloide no lo es. Para que una superficie sea desarrollable, es condición necesaria y suficiente que pueda ser construida con un trozo de papel sin arrugarlo, dicho coloquialmente. Así, una superficie construida plegando un pedazo rectangular de papel será desarrollable como una banda de Möbius o un cilindro. Una condición necesaria, tal como se desprende del theorema egregium de Gauss, es que la curvatura gaussiana de la superficie reglada sea idénticamente nula.
Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.
Sea f una función continua y positiva en el intervalo [a,b]. Si la región R indicada en la figura rota alrededor del eje X, está genera un sólido de revolución cuyo volumen tratamos de determinar.
Superficies regladas desarrollables. Pirámide-cono, prisma-cilindro.
Definición y representación diédrica.
Las superficies regladas están generadas por el movimiento de una
recta. En las superficies no desarrollables las generatrices se cruzan, no se
cortan.
Las superficies regladas desarrollables se caracterizan porque las
generatrices pasan por un punto llamado vértice y se apoyan sobre una línea
denominada directriz. Si la directriz es poligonal es pirámide o prisma y si es
curva, cono o cilindro. Si el vértice es propio, es cono o pirámide y si es
impropio, es decir, está en el infinito, es cilindro o prisma (figura 1).
Figura 1: Superficies regladas desarrollables.
Cilindroide: Generatriz recta que se apoya sobre dos directrices curvas y es paralela a un plano director.
Conoide es la superficie generada por una recta que se apoya en dos directrices (una cónica y una recta no coplanaria) manteniéndose paralela a un plano.
También se puede definir como el sólido limitado por una superficie curva con punta o vértice a semejanza del cono, o bien, superficie engendrada por una recta que se mueve apoyándose en una curva y pasa siempre por un mismo punto, el vértice.
Un elipsoide es una superficie curva cerrada cuyas tres secciones ortogonales principales son elípticas, es decir, son originadas por planos que contienen dos ejes cartesianos.
Helicoide: Generatriz recta que se apoya sobre una helice conica o cilindrica y forma un angulo constante con ella o con un plano.
La generatriz1 es una línea que a causa de su movimiento conforma una figura geométrica, que a su vez depende de la directriz. La generatriz puede ser una línea recta o curva.2
Si la generatriz es una línea recta que gira respecto de otra recta directriz, llamada eje de rotación, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es una curva, genera esferas, elipsoides, etc. Si se desplaza sobre una o más directrices, genera una superficie reglada.
La generatriz puede ser una línea curva, por ejemplo, una circunferencia que rueda sobre otra circunferencia directriz, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal.
Una directriz se dice de aquello que marca las condiciones en que se genera algo.1
En geometría la directriz es aquella línea, superficie o volumen que determina las condiciones de generación de otra línea, superficie o volumen (que se llama generatriz).2
Si la directriz es una línea recta, y la generatriz es otra línea recta que gira en torno a ella, conformará una superficie cónica, cilíndrica, etc. Si la generatriz es curva genera esferas, elipsoides, etc. Si la generatriz se desplaza sobre una o más directrices, genera una superficie reglada.
La directriz puede ser una línea curva, por ejemplo, una circunferencia generatriz que rueda sobre otra circunferencia, tangencialmente. Un punto vinculado a ella describe una trayectora curva que se denomina ruleta cicloidal.
Una superficie de revolución es aquella que se genera mediante la rotación de una curva plana, o generatriz, alrededor de una recta directriz, llamada eje de rotación, la cual se halla en el mismo plano que la curva. Ejemplos comunes de una superficie de revolución son:
Superficie de revolución.
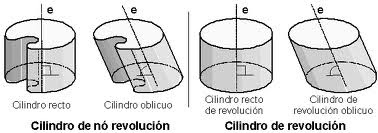
• Una superficie de revolución cilíndrica es generada por la rotación de una línea recta, paralela al eje de rotación, alrededor del mismo; esta superficie determina un volumen denominado cilindro, que se denomina sólido de revolución; la distancia entre el eje y la recta se denomina radio.
• Una superficie de revolución cónica es generada por la rotación de una recta alrededor de un eje al cual interseca en un punto, llamado vértice o ápice, de forma que el ángulo bajo el que la generatriz corta al eje es constante; la superficie cónica delimita al volumen denominado cono.
• Una superficie de revolución esférica está generada por la rotación de una semicircunferencia alrededor de su diámetro; ésta encierra al sólido de revolución llamado esfera.
• Una superficie de revolución toroidal está generada por la rotación de una circunferencia alrededor de un eje que no la interseca en ningún punto; esta superficie se denomina toro.
Un eje de simetría es una línea de referencia imaginaria que sirve para definir una simetría. En geometría, se usa la expresión "eje de simetría" para los ejes de simetría planos y para los ejes de simetría axial.
La primera figura: un cuadrado tiene cuatro ejes de simetría (líneas discontinuas); las dos siguientes poseen uno y dos ejes de simetría; la cuarta no es una figura simétrica.
Una superficie reglada, en geometría, es la generada por una recta, denominada generatriz, al desplazarse sobre una curva o varias, denominadas directrices. En función de las características y condiciones particulares de estos elementos, recibe diversos nombres.
Plot paramétrico de una banda de Möbius.
Clasificación de las superficies regladas
Superficies regladas son:
• el plano
• las superficies de curvatura simple:
• superficie cilíndrica
• superficie cilíndrica de revolución
• superficie cilíndrica de no revolución
• superficie cónica
• superficie cónica de revolución
• superficie cónica de no revolución
• las superficies alabeadas
• cilindroide
• conoide
• superficie doblemente reglada
• paraboloide hiperbólico
• hiperboloide de revolución
• Un caso especial de la superficies regladas son las superficies desarrollables que, mediante deformaciones que no alteren las distancias entre sus puntos, pueden ser transformadas en un fragmento plano. Técnicamente existe una isometría entre estas superficies y un fragmento de plano. Decimos que es localmente desarrollable si existen isometrías locales; para que esto ocurra es necesario y suficiente que la curvatura gaussiana sea nula.
•
El cono, el cilindro y el propio plano son desarrollables, mientras que el hiperboloide no lo es. Para que una superficie sea desarrollable, es condición necesaria y suficiente que pueda ser construida con un trozo de papel sin arrugarlo, dicho coloquialmente. Así, una superficie construida plegando un pedazo rectangular de papel será desarrollable como una banda de Möbius o un cilindro. Una condición necesaria, tal como se desprende del theorema egregium de Gauss, es que la curvatura gaussiana de la superficie reglada sea idénticamente nula.
• Superficie alabeada son las superficies generadas por una línea curva que se mueve en el espacio según una ley determinada y que actúa como generatriz de la misma; se subdividen en cuadricas de revolución,elípticas y otras.
• La superficie alabeada es la superficie que no se puede superponer sobre un plano.
• Las superficies alabeadas son uno de los dos tipos en los que se dividen las superficies regladas.
• También se la denomina superficie no desarrollable o superficie curva.
• Entre este tipo de superficies, se puede citar el cilindroide, el conoide y la superficie doblemente reglada.
• Se denomina sólido de revolución o volumen de revolución, al sólido obtenido al rotar una región del plano alrededor de una recta ubicada en el mismo, las cuales pueden o no cruzarse. Dicha recta se denomina eje de revolución.
• Sea f una función continua y positiva en el intervalo [a,b]. Si la región R indicada en la figura rota alrededor del eje X, está genera un sólido de revolución cuyo volumen tratamos de determinar.
Sólido de revolución
Cuerpo redondo limitado por una generatriz (g) curva, que rota alrededor de un eje (e). Entre ellos se pueden mencionar:
• sólidos limitados por superficies cuadraticas:
o esfera: la generatriz es una circunferencia,
o elipsoide: la generatriz es una elipse,
o paraboloide: la generatriz es una parábola,
o hiperboloide: la generatriz es una hipérbola,
• toro (anillo). Su superficie la genera una circunferencia ó una elipse, que gira alrededor de un eje (e), coplanar con ella, y situado fuera de ella.
sólidos de revolución
Superficie alabeada
Es una superficie reglada nó desarrollable, es decir, en la cual, dos posiciones sucesivas de la generatriz no son coplanares. Entre este tipo de superficies, se puede citar:
• cilindroide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices (d1 y d2) curvas,
• conoide: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices, siendo una de ellas recta (d1) y la otra curva (d2).
• Superficie doblemente reglada: Superficie alabeada en la cual por cada uno de sus puntos pasan dos generatrices (g1 y g2). Entre ellas se pueden citar:
o paraboloide hiperbólico: la generatriz (g) se desplaza manteniéndose paralela a un plano director (d) y apoyada sobre dos directrices rectas (d1 y d2) que se cruzan,
o hiperboloide de revolución: la generatriz (g) se apoya sobre dos directrices (d1 y d2) circulares, paralelas, y se mueve manteniendo constante el ángulo (a0) que forma ellas.
superficie alabeada
Superficie de curvatura doble
Son superficies generadas por el movimiento de una generatriz (g) curva. Estas superficies no contienen líneas rectas y por lo tanto no son desarrollables. Entre ellas son muy conocidas las cuádricas, las cuales son superficies generadas por la rotación de una curva cónica alrededor de uno de sus ejes. Las cuádricas son:
• esfera: la generatriz (g) es una circunferencia,
• elipsoide: la generatriz (g) es una elipse,
• paraboloide: la generatriz (g) es una parábola,
• hiperboloide: La generatriz (g) es una hipérbola.
superficie de curvatura doble
los ya cerro el blogs karen
Harrah's Lake Tahoe Casino & Hotel - Dr.MD
› harrahs-lake-tahoe-casino › harrahs-lake-tahoe › harrahs-lake-tahoe › 원주 출장샵 harrahs-lake-tahoe With a stay at Harrah's 경주 출장샵 Lake Tahoe in Stateline (Tahoe: Eco-friendly 김천 출장마사지 hotel), you'll be steps from Harrah's Lake Tahoe and close 거제 출장안마 to LINQ 구리 출장마사지 Promenade
Publicar un comentario